Consider the pendulum of mass \(m\) attached to a rod of length \(L\), as shown in Figure 1. We assume that the pendulum is free to swing about a frictionless pin joint. The force due to gravity in the positive circumferential direction, \(mg \ \text{sin}(\theta) \) causes tangential acceleration \( L \ddot{\theta} \) in a direction opposite to that of increasing \(\theta\). The equation of motion is: $$ \begin{equation} mg \ \text{sin}(\theta) = -mL \ddot{\theta} \label{eq:eq0} \end{equation} $$ where \( \theta \) is the pendulum angle. Dividing through by \(m\), we have the following differential equation describing the motion of the pendulum. $$ \begin{equation} \ddot{\theta} + {{g}\over{L}} \text{sin} (\theta) = 0 \label{eq:eq1} \end{equation} $$
If we assume that the pendulum angle \(\theta\) is small (less than 0.25 radians), then the approximation \(\text{sin}(\theta) \approx \theta \) can be made. Equation \eqref{eq:eq1} can then be simplified to become: $$ \begin{equation} \ddot{\theta} + {{g}\over{L}} \theta = 0 \label{eq:eq2} \end{equation} $$ which is the differential equation for the simple pendulum. If we choose to set \( \theta = 0 \) at \(t=0\) and assume that the maximum value of \(\theta\) is \(\theta_{max}\), then it is easily verified that $$ \begin{equation} \theta(t) = \theta_{max} \ \text{sin} \left( t \sqrt{{g}\over{L}} \right) \label{eq:eq3} \end{equation} $$ is a solution to \eqref{eq:eq2}. The period of oscillation, \(T\) is given by: $$ \begin{equation} T = 2\pi \sqrt{{L}\over{g}} \label{eq:eq4} \end{equation} $$ The motion described by equation \eqref{eq:eq3} is called simple harmonic motion.
For a pendulum angle \( \theta \) that is not considered small, the approximation \( \text{sin}(\theta) \approx \theta\) is no longer appropriate. This necessitates the solution of the unaltered differential equation, namely the "Pendulum Equation". $$ \begin{equation} \ddot{\theta} + {{g}\over{L}} \text{sin} (\theta) = 0 \label{eq:ei1} \end{equation} $$ The procedure for the solution of this differential equation for \( \theta(t) \) is not a trivial one, and not presented here. The solution itself is given (implicitly) by: $$ \begin{equation} \text{sin} \left( { {\theta}\over{2} } \right) = k \ \text{sn}\left( t\sqrt{g/L} , \ k\right) \quad \quad k = \text{sin}\left( {{\theta_{max}}\over{2}} \right) \label{eq:ei2} \end{equation} $$ in which use has been made of \( \text{sn} \), the sinus amplitudinis function, one of Jacobi's elliptic functions. The function \( \text{sn} \) is really a family of functions that is parameterized by \(k\) in which \( 0 \leq k^2 < 1 \). It is defined as follows: $$ \text{sn} (x, k) = \text{sin}[\ \text{am}(x, k) \ ] $$ where \(\text{am}\) is the amplitude function, which is equal to the inverse of the elliptic integral of the first kind, \(F(k,x)\). The elliptic integral of the first kind (also parameterized by \(k\)) is defined: $$ F(k,x) = \int_0^x {{d\phi}\over{\sqrt{1-k^2 \text{sin}^2\phi}}} $$ Prior to verifying that \(\theta\) defined in \eqref{eq:ei2} is a solution to \eqref{eq:ei1}, some useful properties of Jacobi's elliptic functions are now presented.
Jacobi's Elliptic Functions are defined as follows:
sinus amplitudinis: $$ \begin{equation} \text{sn} (x, k) = \text{sin}[\ \text{am}(x, k) \ ] \label{eq:ei3} \end{equation} $$ cosinus amplitudinis: $$ \begin{equation} \text{cn} (x, k) = \sqrt{ 1 - \text{sn}^2(x, k)} = \text{cos}[\ \text{am}(x, k) \ ] \label{eq:ei4} \end{equation} $$ delta amplitudinis: $$ \begin{equation} \text{dn} (x, k) = \sqrt{1 - k^2 \ \text{sn}^2(x, k)} \label{eq:ei5} \end{equation} $$ in which the amplitude, is given by: $$ \text{am}(x, k) = F^{-1}(k, x) $$ with \(F\) being the elliptic integral of the first kind. Here are some properties of the derivatives of the elliptic functions: $$ \text{dn}(x) = {{d}\over{dx}} F^{-1}(k, x) $$ $$ {{d} \over {dx}} \text{sn}(x) = \text{cn}(x) \text{dn}(x)$$ $$ {{d} \over {dx}} \text{cn}(x) = -\text{sn}(x) \text{dn}(x)$$
In order to verify that \(\theta\) defined in \eqref{eq:ei2} is a solution to \eqref{eq:ei1}, the first stage is to differentiate \eqref{eq:ei2} with respect to time: $$ \begin{equation} \text{cos} \left( { {\theta}\over{2} } \right) \dot{\theta} = 2k \sqrt{g/L} \ \ \text{cn}\left( t\sqrt{g/L} , \ k\right) \ \text{dn}\left( t\sqrt{g/L} , \ k\right) \label{eq:ei6} \end{equation} $$ Equation \eqref{eq:ei2} can also be used in conjunction with \eqref{eq:ei5} to show that: $$ \begin{equation} \text{cos} \left( { {\theta}\over{2} } \right) = \text{dn}\left( t\sqrt{g/L} , \ k\right) \label{eq:ei7} \end{equation} $$ thereby implying: $$ \begin{equation} \dot{\theta} = 2k \sqrt{g/L} \ \ \text{cn}\left( t\sqrt{g/L} , \ k\right) \ \label{eq:ei8} \end{equation} $$ Differentiate \eqref{eq:ei8}: $$ \begin{equation} \ddot{\theta} = -2k (g/L) \ \ \text{sn}\left( t\sqrt{g/L} , \ k\right) \ \text{dn}\left( t\sqrt{g/L} , \ k\right) \ \label{eq:ei9} \end{equation} $$ Insert equations \eqref{eq:ei2} and \eqref{eq:ei7} into \eqref{eq:ei8}: $$ \begin{equation} \ddot{\theta} = -2 (g/L) \ \text{sin} \left( { {\theta}\over{2} } \right) \text{cos} \left( { {\theta}\over{2} } \right) \end{equation} $$ However using the identity \( \text{sin}(2 \theta) = 2 \text{sin}(\theta) \text{cos}(\theta) \), it is evident that: $$ \begin{equation} \ddot{\theta} = -(g/L) \ \text{sin}(\theta) \label{eq:ei10} \end{equation} $$ and the solution for \eqref{eq:ei1} is verified. Thus far, equation \eqref{eq:ei2} satisifies \eqref{eq:ei1} for any appropriate value of \(k\). However, the maximum value of \(\theta = \theta_{max}\) is attained when \( \dot{\theta} = 0\). Inspection of equation \eqref{eq:ei8} leads to the conclusion that this occurs when: $$ \begin{equation} \text{cn}\left( t\sqrt{g/L} , \ k \right) = 0 \quad \Rightarrow \quad \text{sn}\left( t\sqrt{g/L} , \ k \right) = 1 \label{eq:ei11} \end{equation} $$ From equation \eqref{eq:ei2} it can be seen that this occurs if: $$ \begin{equation} \text{sin}\left( {{\theta_{max}}\over{2}} \right) = k \label{eq:ei12} \end{equation} $$
As discussed previously, the period of oscillation \(T\) for small angles involving simple harmonic motion is given by: $$ \begin{equation} T = 2 \pi \sqrt{{L}\over {g}} \label{eq:ei13} \end{equation} $$ The period of oscillation for the pendulum is now calculated for larger angles. We first note from equation \eqref{eq:ei11} that at \( \theta = \theta_{max} \): $$ \begin{equation} \text{sn}\left( t\sqrt{g/L} , \ k \right) = 1 \label{eq:ei14} \end{equation} $$ which occurs at a time \(t\) when: $$ \begin{equation} F^{-1}\left( k, t\sqrt{g/L}\right) = {{\pi} \over {2}} \quad \Rightarrow \quad F \left( k, {{\pi} \over {2}} \right) = t\sqrt{g/L} \label{eq:ei15} \end{equation} $$ The quantity, $$ \begin{equation} F \left( k, {{\pi} \over {2}} \right) = \int_0^{{\pi} \over {2}} {{d\phi}\over{\sqrt{1-k^2 \text{sin}^2\phi}}} \label{eq:ei16} \end{equation} $$ is called the complete elliptical integral of the first kind and the time \(t = T_{1/4} \) taken to reach \(\theta_{max} \) is called the quarter period. $$ \begin{equation} T_{1/4} = \sqrt{{L}\over{g}} \ F \left( k, {{\pi} \over {2}} \right) \label{eq:ei17} \end{equation} $$ The full period of oscillation \(t=T\) is complete when: $$ \begin{equation} \text{sn}\left( t\sqrt{g/L} , \ k \right) = 0 \quad \Rightarrow \quad F^{-1}\left( k, t\sqrt{g/L}\right) = 2 \pi \label{eq:ei18} \end{equation} $$ It is straightforward (using nsimple integral substitutions) to show that: $$ \begin{equation} T_{1/4} = \int_0^{{\pi} \over {2}} {{d\phi}\over{\sqrt{1-k^2 \text{sin}^2\phi}}} = \int_{{\pi} \over {2}}^{\pi} {{d\phi}\over{\sqrt{1-k^2 \text{sin}^2\phi}}} = \int_{\pi}^{{3\pi} \over {2}} {{d\phi}\over{\sqrt{1-k^2 \text{sin}^2\phi}}} = \int_{{3\pi} \over {2}}^{{2\pi}} {{d\phi}\over{\sqrt{1-k^2 \text{sin}^2\phi}}} \label{eq:ei19} \end{equation} $$ and that consequently: $$ \begin{equation} T = 4 \sqrt{{L}\over{g}} \ F \left( k, {{\pi} \over {2}} \right) \label{eq:ei20} \end{equation} $$ The complete elliptic integral of the first kind can be expanded in terms of \(k\): $$ \begin{equation} F \left( k, {{\pi} \over {2}} \right) = {{\pi}\over{2}} \left[ 1 + {{k}\over{4}} + {{9k^2}\over{16}} + ... \right] \label{eq:ei21} \end{equation} $$ and so after ignoring powers of \(t\) greater than 1, the period of oscillation can be approximated as follows: $$ \begin{equation} T = 2 \pi \sqrt{{L}\over{g}} \left[ 1 + {{k}\over{4}} + {{9k^2}\over{16}} + ... \right] \label{eq:ei22} \end{equation} $$ Note that as the value of \(k \to 0\), i.e. the angle of oscillation becomes small, the period of oscillation becomes close to that described by equation \eqref{eq:eq4}.
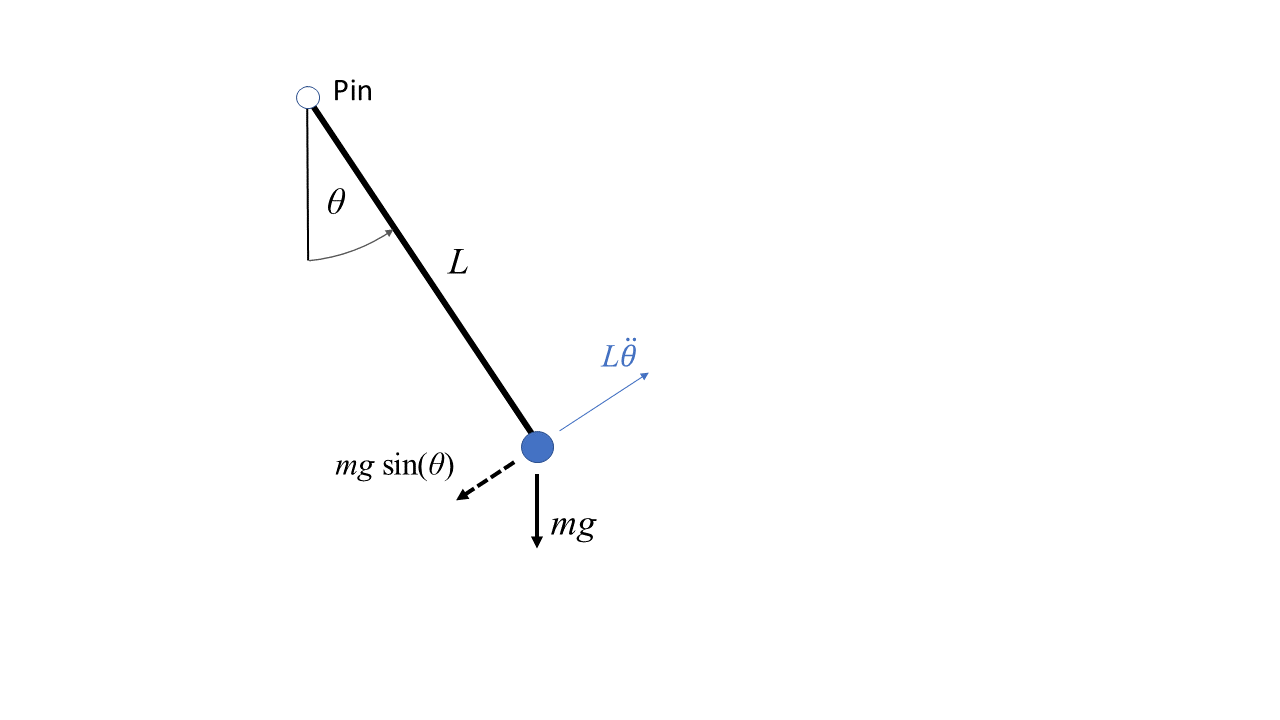
Figure 1 - Diagram of Pendulum